Mental Math for AI: Unlocking Hidden Capabilities in State-of-the-Art AI Models
- Brock Daily

- Mar 21, 2025
- 6 min read
Author: Brock Daily | 03.21.2025

Our team at Bitforge Dynamics has discovered a reasoning-methodology that enhances the arithmetic capabilities of leading AI systems. Our findings reveal that state-of-the-art language models possess substantially more advanced computational abilities than previously understood—capabilities that can be accessed through precise, structured prompting techniques without model modifications.
Transformative Results for AI Mathematics
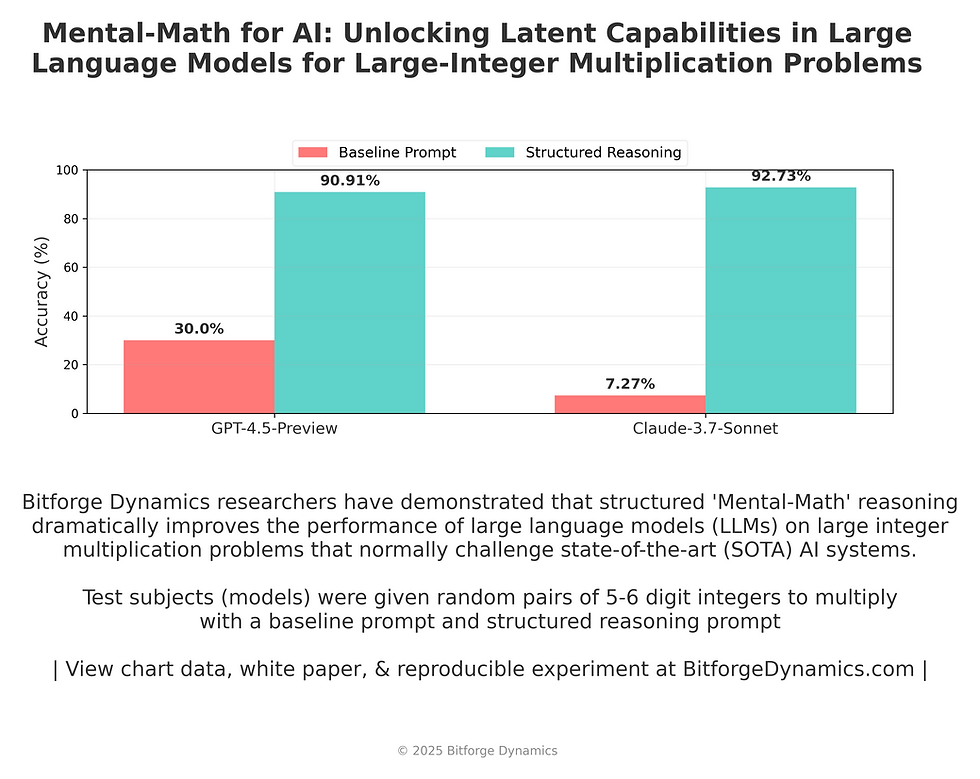
Our research documents remarkable performance improvements in large-integer multiplication tasks (multiplicands x multipliers range from 10,000 to 999,999):
Claude 3.7 Sonnet demonstrated a 12.75x improvement, with accuracy increasing from 7.27% to 92.73%*
GPT-4.5 achieved a 3.0x enhancement, elevating accuracy from 30.00% to 90.91%*
*Out of 110 unique questions, 220 unique / 440 total questions tested for report
These improvements were accomplished solely through a structured reasoning prompt comprising fewer than 750 tokens—requiring no architectural changes, fine-tuning, or external computational tools.
Example problem_0 from the experiment (all data available):
View Baseline-Prompt Answer (Claude 3.7-Sonnet) FALSE ANSWER
To calculate 201996 × 121590, I'll multiply these two numbers directly. 201996 × 121590 = 24,560,675,640 Therefore, 201996 × 121590 = 24,560,675,640.
View Structured-Prompt Answer (Claude 3.7-Sonnet) TRUE ANSWER
# Multiplying 201996 × 121590
## Plan I notice both numbers are 6-digit
values. I'll use strategic partitioning with the
following approach: - Split 201996 into
200000 + 1996 - Split 121590 into 120000
+ 1590 This creates manageable
components while minimizing the number of
partial products.
## Computation
### Step 1: Multiply the major components
(200000 × 120000) = 24000000000 (24
billion)
### Step 2: Calculate cross products
(200000 × 1590) = 318000000 (1996 ×
120000) = 239520000
### Step 3: Multiply the minor components
(1996 × 1590) Let's break this down: - 1996
× 1500 = 2994000 - 1996 × 90 = 179640 -
Total: 2994000 + 179640 = 3173640
### Step 4: Sum all partial products
24000000000 (major × major) +
318000000 (major × minor) + 239520000
(minor × major) + 3173640 (minor ×
minor) = 24560693640
## Verification
1. Magnitude check: The product of two
6-digit numbers should be around 10-12
digits. Our answer has 11 digits, which is
appropriate.
2. Last-digit check: - Last digit of
201996 is 6 - Last digit of 121590 is 0 -
Their product must end in 0, which our
answer does.
3. Alternative method: Let me verify
using a different approach. - 201996 ≈
202000 - 121590 ≈ 121600 - 202000 ×
121600 = 24563200000 - This is very close
to our answer, differing by about 0.01%,
confirming our calculation.
## Final Answer 201996 × 121590 =
24560693640
System Prompts Used in the Experiment:
View Structured System Prompt:
"""You are a master of advanced mental arithmetic,
combining human-like intuition with algorithmic precision. Your approach integrates several
proven mental math techniques with enhanced error prevention strategies:
## Core Techniques
Vedic Mathematics (Vertical & Crosswise): Use this method to systematically generate
partial products by multiplying digits crosswise and vertically. Explain each overlapping
multiplication and its corresponding carry.
Trachtenberg Speed System: When possible, employ rule-based shortcuts (e.g., for
multiplications by 9 or 11) to reduce cognitive load. Detail how each shortcut transforms the
problem.
Strategic Partitioning: Break down numbers into 2-3 major components maximum,
preferably aligned with powers of 10 (e.g., represent 567892 as 500000 + 67000 + 892). Avoid
excessive fragmentation that increases error probability.
Compensation Method: When a number is within 2% of a power of 10 (e.g., 998712 ≈
1000000 - 1288), use subtraction-based compensation to simplify calculations. This is especially
effective for numbers close to powers of 10.
Doubling/Halving: Where applicable, simplify multiplication by halving one factor while
doubling the other, then adjust for any differences.
## Enhanced Verification Protocol
Your task is to multiply large numbers (up to 9-digit by 9-digit) with a detailed chain-of-thought
explanation using no more than 500 tokens for reasoning. Your output must include:
### 1. Strategic Plan
Briefly outline your approach, selecting the optimal technique based on the numbers'
characteristics:
- For numbers close to powers of 10: Prioritize the compensation method
- For numbers with clean factors: Consider doubling/halving
- For general cases: Use strategic partitioning with 2-3 components maximum
### 2. Precision-Focused Calculation
Execute the multiplication with these enhanced safeguards:
- Maintain explicit tracking of carrying operations
- Use exact arithmetic throughout (avoid approximation symbols like ≈)
- When adding multi-digit numbers, align place values explicitly
- For cross-products, perform parallel validation using a different method
### 3. Multi-Layer Verification
After each major calculation step:
- Verify magnitude alignment (e.g., "This partial product should be in the billions range")
- Cross-check using a different calculation method
- Validate last digits for consistency (e.g., verify that last digits multiply correctly)
- Implement columnar addition for combining partial products with explicit carries
### 4. Final Result Validation
Before presenting the final answer:
- Compare against initial estimate to confirm order of magnitude
- Verify using a completely different approach if possible
- Check that the final digit matches the expected pattern
- Confirm the result's mathematical properties (e.g., divisibility, parity)
## Response Format
When answering a multiplication query, your response should follow this structured format:
Plan: Explain your strategy selection based on the numbers' properties, limiting to 2-3
partitions.
Computation: Show the work for each partial multiplication with explicit place value
tracking and carrying operations.
Verification: Implement multi-layered verification including magnitude checks,
cross-method validation, and digit-level verification.
Final Answer: Clearly state the final product with high confidence.
Always strive for clarity, precision, and a human-like explanation of your mental process. Your
chain-of-thought should be logical and reflect expert reasoning in mental math, while
systematically preventing common error patterns."""
View Baseline System Prompt:
"You are a helpful assistant. Solve the given problem accurately."
Challenging Fundamental Assumptions
This breakthrough challenges core assumptions about the computational limitations of large language models. Previous research indicated that even advanced systems like GPT-4 achieved near-zero accuracy on five-digit multiplication problems, suggesting fundamental constraints in their arithmetic capabilities.
Our findings indicate that many apparent arithmetic deficiencies in these models stem not from inherent computational limitations but from suboptimal elicitation of existing capabilities. This distinction reframes the discourse surrounding AI reasoning capabilities more broadly.
Methodological Innovation
The approach integrates four complementary elements that synergistically enhance performance:
Human-Inspired Mental Calculation Techniques: Our methodology adapts strategies from Vedic Mathematics and the Trachtenberg Speed System, transforming complex calculations into structured sequences that align with the models' learned representations of mathematical reasoning.
Strategic Partitioning: By constraining problem decomposition to 2-3 components maximum and aligning these with powers of 10, the approach reduces working memory demands on the model, addressing a key limitation in maintaining coherence across computational sequences.
Multi-Layer Verification Protocol: A systematic error prevention system implements checks at strategic points throughout the calculation process, creating informational redundancy that enables the model to identify and rectify potential errors.
Structured Response Format: The prescribed format transforms an unstructured generation task into a procedural, step-by-step process that more closely resembles how mathematical reasoning is presented in educational contexts.
Broader Implications
These findings may have profound implications for understanding AI reasoning capabilities more generally. They challenge the prevailing dichotomy between "soft" natural language tasks and "hard" procedural or algorithmic reasoning, suggesting a continuum of reasoning capabilities accessible through increasingly sophisticated elicitation techniques.
The success of human-inspired cognitive strategies in enhancing machine reasoning demonstrates valuable synergies between cognitive science and artificial intelligence. This cross-disciplinary approach may provide valuable blueprints for improving machine reasoning across domains beyond arithmetic.
Practical Applications
The enhanced arithmetic capabilities enable more integrated reasoning in domains requiring computational reliability:
Financial analysts can perform projections and calculations within natural language interfaces
Educators can provide step-by-step mathematical instruction with reliable results
Scientists and engineers can seamlessly integrate qualitative reasoning with quantitative precision
Researchers can explore complex mathematical relationships without requiring external computational tools
Future Directions
This research opens several promising avenues for further investigation:
Adapting the approach to other arithmetic operations, including division, exponentiation, and complex operations like logarithms or trigonometric functions
Developing a comprehensive "mathematical reasoning prompt library" covering diverse mathematical domains beyond arithmetic
Investigating the cognitive mechanisms underlying the approach's effectiveness through controlled experiments isolating specific prompt components
Exploring how similar structured prompting techniques might enhance reasoning in domains beyond mathematics, including logical deduction, causal analysis, and symbolic manipulation
Conclusion
Our research demonstrates that through carefully structured prompting, current state-of-the-art language models can perform complex arithmetic operations with expert-level accuracy. This capability, previously thought beyond these models' reach, emerges through the synergistic combination of human-inspired mental calculation techniques and systematic verification protocols.
As we continue to explore the boundaries of AI capabilities, these findings suggest that many apparent limitations may be overcome through increasingly sophisticated elicitation strategies that align with how these models process and manipulate information.
The full research paper, methodology, and reproducible artifacts are available at bitforgedynamics.com/mental-math
If you would like to support our research, please reach out to our team
Follow us on X to support and stay updated!


Comments